Σημαντικές επισημάνσεις στις αντίστροφες συναρτήσεις και τις ένα προς ένα μαθηματικά γ λυκείου προσανατολισμού

Παρακάτω δίνεται ένα μικρό τμήμα της θεωρίας που αφορά την αντίστροφη συνάρτηση και την συνάρτηση ένα προς ένα (1-1 ).

Στόχος είναι να θυμήσει μερικές ιδιότητες που είναι απαραίτητες σε σχετικές με αυτή ασκήσεις.

Πως αποδεικνύω ότι μια συνάρτηση δεν είναι ένα προς ένα,λυμένο παράδειγμα μαθηματικά γ λυκείου προσανατολισμού

Στο παρακάτω παράδειγμα θα δείξουμε έναν από τους τρόπους  που μπορούμε να αποδείξουμε ότι   μια  συνάρτηση δεν είναι ένα προς ένα.

'Ασκηση
Να αποδείξετε ότι η συνάρτηση     με 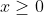 δεν είναι  "1-1"

Να εξετάσετε αν η συνάρτηση είναι ένα προς ένα ,λυμένο παράδειγμα μαθηματικά γ λυκείου προσανατολισμού

Σε προηγούμενη  ανάρτηση αποδείξαμε πως μια συνάρτηση δεν είναι  ένα προς ένα με μια συγκεκριμένη διαδικασία.
Στο παρόν άρθρο θα  δούμε πως αποδεικνύουμε  πότε μια συνάρτηση δεν είναι ένα προς ένα  δίνοντας ακόμα έναν τρόπο.

'Ασκηση
Να αποδείξετε ότι η συνάρτηση f(x)=|x+5|-1  δεν είναι ένα προς ένα.

Λύση

Α τρόπος (Αλγεβρικά )

Αν   βάλω χ=-6  : f(x)=|-6+5|-1 =0
Αν βάλω επίσης χ=-4 : f(x)=|-4+5|-1 =0.
Παρατηρώ ότι  f(-6)=f(-4)=0   ενώ  το 
Βγάζω το συμπερασμα ότι η συνάρτηση  f(x)  δεν είναι "1-1"

Β τρόπος (Γραφικά )

Εδώ πρέπει να θυμάσαι ότι μια συνάρτηση είναι ένα  προς ένα  όταν κάθε παράλληλη ευθεία προς τον άξονα χχ' τέμνει την γραφική παράσταση της συνάρτησης σε ένα σημείο.

Για την άσκησή μας τώρα όπου η f(x)=|x+5|-1 έχει απόλυτα θα κάνουμε άρση απολύτων .

Η γραφική της παράσταση είναι :

Εύκολα καταλαβαίνουμε ότι μια ευθεία παράλληλη προς τον άξονα χχ' δεν την τέμνει σε ένα σημείο .

'Αρα η συνάρτηση δεν είναι ένα προς ένα.